문제
1011번: Fly me to the Alpha Centauri
우현이는 어린 시절, 지구 외의 다른 행성에서도 인류들이 살아갈 수 있는 미래가 오리라 믿었다. 그리고 그가 지구라는 세상에 발을 내려 놓은 지 23년이 지난 지금, 세계 최연소 ASNA 우주 비행
www.acmicpc.net
1. 첫 번째 풀이
사고 과정
- 뒤로 가는 건 볼 필요도 없을 것 같다. 첫 시작에 -1을 가면 -2, -1, 0을 움직일 수 있으니, 앞으로 나아갈 수 없다.
- 중간에 1칸 적게 가는 경우는, 해당 칸과 그전 칸의 순서를 바꿔도 유지된다. 그러니 비내림차순이라 생각하자.
- 일단 1부터 시작해 답이 어떻게 되는지 알아보자. n칸에 몇 번 움직일까?
1: 1
2: 1 1
3: 1 1 1
4: 1 2 1
5: 1 2 1 1
6: 1 2 2 1
7: 1 2 1 2 1
8: 1 2 2 2 1
9: 1 2 3 2 1
10: 1 2 2 2 2 1
상당히 대칭적이다. 뭔가 규칙이 보이는 것 같은데? 개수를 표로 정리해 보자.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 5 | 6 |
10~20도 한 번 세보자.
11: 1 2 2 3 2 1
12: 1 2 3 3 2 1
13: 1 2 3 3 2 1 1
14: 1 2 3 3 2 2 1
15: 1 2 3 3 3 2 1
16: 1 2 3 4 3 2 1
17: 1 2 3 4 3 2 1 1
18: 1 2 3 4 3 2 2 1
19: 1 2 3 4 3 3 2 1
20: 1 2 3 4 4 3 2 1
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 6 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 |
21은 다시 9번이다.
우선 로직으로 짜볼 수 있을 것 같다.
1. int T, x, y, d, n, o, max 선언(T, x, y, y - x, 칠할 값, 칠할 칸, n으로 칠할 수 있는 최댓값)
2. T를 입력받아 T번 반복
3. x, y를 입력받고, x - y를 캐싱 (y가 2^31 이하니, int 사용 가능)
이후 작성할 글이 있다면 추가 작성
코드
#include <stdio.h>
int main() {
int t, x, y;
scanf("%d", &t);
while (t--) {
scanf("%d %d", &x, &y);
int d = y - x, n = 1, o = 1, max;
for (max = 1; max < d; max += o) {
if (n % 2 == 0) {
o++;
}
n++;
}
printf("%d\n", n);
}
}결과

출력값은 꽤 정확했는데, 시간 초과가 떴다.
2. 두 번째 풀이 (마지막 풀이)
사고 과정
- 가장 좋은 건 역시, y - x에 특정 연산을 해서 한 번에 찾아내는 것.
- 새 값이 들어오는 숫자만 모으면? 1, 2, 3, 5, 7, 10, 13, 17, 21... 역시나 그들의 차가 1, 1, 2, 2, 3, 3, 4, 4일뿐이다.
- 결국 피라미드 형탠데, 끝에서부터 잘라낸다? 아니다. 그건 첫 번째와 다를 바가 없다.
- 결국 수는 1 2 1, 1 2 3 2 1 같은 피라미드 형태로 나타난다.
- 값이 바뀌는 순간은, 피라미드가 모두 다 차는 순간...
- 피라미드를 반으로 나눠서 계산해 보면 어떨까?
- 1, 1 2, 1 2 3... 마다 꽉 찬다.
- 1부터 n까지의 합? 이걸 구하는 공식은 n(n+1) / 2. 어?
- 피라미드를 반 갈라서 위 공식을 쓰는 거니, / 2는 상쇄되고 n(n+1)만 남는다.
- 각 답의 마지막 숫자를 적어보면 1, 2, 4, 6, 9, 12, 16, 20. 이는 1x1, 1x2, 2x2, 2x3, 3x3, 3x4, 4x4, 4x5다.
- 각각 정답은 1, 2, 3, 4, 5, 6, 7, 8. nxn으로 보면 n, n+1, n+1, 2n, 2n-1, 2n, 2n-1, 2n... 아, 이렇게 쓰는 게 맞겠다.
- 2n-1, 2n, 2n-1, 2n, 2n-1. 이렇게 보는 게 맞겠다.
- 그럼 n은 어떻게 구할 수 있을까? y - x의 제곱근이 곧 n이 된다. 단, 제곱수인 경우엔 예외가 된다.
- 간단한(?) 연산과 조건문이면 문제를 풀 수 있을 것 같다.
- n이 2일 때, 4는 3, 5 ~ 6은 4, 7 ~ 9는 5다. 2n-1, 2n, 2n+1.
- n이 4일 때, 16은 7, 17 ~ 20은 8, 21 ~ 25는 9다. 2n-1, 2n, 2n+1.
- 세 가지 경우의 수를 따지면 될 것 같다.
- 아니지. 애초에 sqrt 연산할 때 1을 빼고 넣는다면?
- 16일 때 3, 17일 때 4, 26일 때 5가 나온다. 이중 마지막은 다음 칸으로 넘어가니, 2개의 조건문이면 충분하다.
- 다르게는 삼항 연산자로 표현할 수 있게 된다.
- sqrt 함수의 연산 시간이 걱정되지만, 2^31 - 1을 넣어본 결과 순식간에 계산했으니 믿고 간다.
1. T를 입력받고 T만큼 반복
2. x, y를 입력받은 후 y - x 계산, d에 저장
3. (d-1)의 제곱근 n을 구하고, d가 n * (n + 1) 이하라면 2n, 초과하면 2n + 1을 출력
코드
#include <stdio.h>
#include <cmath>
int main() {
int t, x, y;
scanf("%d", &t);
while (t--) {
scanf("%d %d", &x, &y);
int d = y - x, n = std::sqrt(d - 1);
printf("%d\n", (d <= n * (n + 1)) ? 2 * n : 2 * n + 1);
}
}- 값은 정확할까? 첫 번째 풀이의 출력과 비교해 보자.


- 값도 확실하다. 바로 제출해 보자.
결과

초고속 정답!
개선
사고 과정
- 어디를 더 개선시킬 수 있을까?
- t번 반복은 while(t--)가 가장 깔끔하니 통과.
- d, n을 캐싱하지 않아도 될까? 하지만 d는 2번, n은 꽤 많이 사용됐으니 지우기도 애매하다.
- 그나마 d는 없애도 될 법 하지만, 반대로 굳이 지울 이유도 없다.
- 딱히 개선점을 찾진 못 하겠다.
가장 효율적인 코드
https://www.acmicpc.net/source/29450014
jinhan814님의 코드. C언어로 156 KB밖에 쓰지 않는 기적을 보여주셨지만,,, 너무 나노 단위까지 접근하셔서 알고리즘 분석보다 코드 분석이 더 오래 걸릴 것 같다.
https://www.acmicpc.net/source/63848524
diguq0107님의 코드. 코테 특유의 암호 코드지만, 적당히 행간을 나눠보면 분석할만하다.
내 코드와 비교
1. 나는 d로, 이 분은 n으로 같은 값을 뒀다. 설명은 n으로 적겠다.
2. 핵심 로직은 n이 0 이하가 될 때까지 n -= (1 + i++) / 2. 어떻게 답이 구해지는 걸까?
- n에서 빠지는 수를 나열해 보자. 1, 1, 2, 2, 3, 3, 4, 4, 5, 5.... 진짜 왜 되는 거지?
- 아. 중간에 하려던 것과 같구나. 피라미드를 양 끝에서 잘라내는 방식이다.
- 그럼 여기서 의문. 왜 양끝에서 잘라내는 건 되고, 1부터 올라가는 건 안 되던 걸까?
- 첫 번째 풀이와 diguq0107님의 코드 간 차이를 찾아라.
- 우선 변수가 하나 더 사용됐고, 이 분의 연산은 ++, /, -로 매 회 세 가지가 돌아간다.
- 내 코드엔 ++, ++, +, % 네 가지 연산이 들어간다.
- 내 코드는 2,147,483,647을 넣었을 때 뻗다시피 느렸고, diguq0107님의 코드는 순식간에 계산됐다.
실험 1
- % 연산이 느린가?
- diguq0107님의 코드를 응용해 / 연산으로 바꿔보자.
코드
#include <stdio.h>
int main() {
int t, x, y;
scanf("%d", &t);
while (t--) {
scanf("%d %d", &x, &y);
int d = y - x, max = 0, n;
for (n = 1; max <= d; max += (1 + n++) / 2);
printf("%d\n", n);
}
}차이라곤 - 냐 + 냐 정도뿐이다.
결과

이대로 스탑. 범인은 %가 아닌 +였던 걸까?
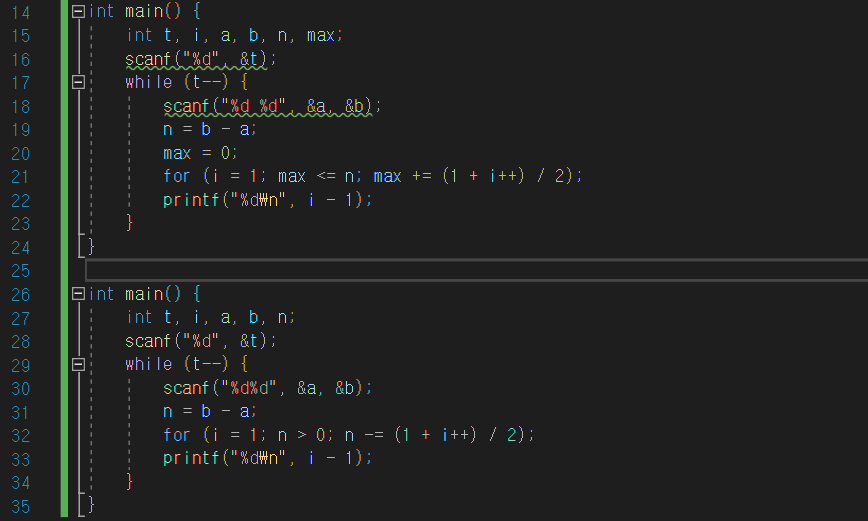
더 쉬운 비교를 위해 최대한 비슷하게 코드를 바꿔보았다. 그럼에도 위 코드는 영겁의 시간이, 아래 코드는 찰나의 순간이 필요했다.
실험 2
- chatGPT에게 물어보면 정답을 알려줄까?
- 사실 말이 실험이지, 한 번 물어보았다.

- 두 번째 코드는 n이 음수가 되는 순간 무조건 반복이 중단되지만, 첫 번째 코드는 max > n인 상황에서도 반복문이 돌아간다고 한다.
- 잘 이해가 안 가서, 좀 더 자세히 설명해 달라고 요청해 보았다.

- 사실 이 설명을 보고도 원리가 잘 이해가 안 간다. 두고두고 읽고 검색해 보며 이해해 봐야겠다.
강평
재밌는 수학 문제. 골드 5 답게 어렵진 않지만, for문에 관한 새로운 사실 하나를 알게 되었다. 역시 문제를 푼 후에 코드 비교를 해보는 게 제일 중요한 것 같다.
단순히 +냐 -냐로 시간이 이렇게 다이나믹하게 변하니, 앞으로 코드짤 때 잘 응용해야겠다.
'코딩테스트 > 백준' 카테고리의 다른 글
| [백준/C++] 1027번. 고층 건물 (0) | 2023.08.30 |
|---|---|
| [백준/C++] 1043번. 거짓말 (0) | 2023.08.30 |
| [백준/C++] 1016번. 제곱 ㄴㄴ 수 (0) | 2023.08.26 |
| [백준/C++] 1015번. 수열 정렬 (0) | 2023.08.26 |
| [백준/C++] 1094번. 막대기 (0) | 2023.08.23 |



