서론
현재 개발 중인 게임의 튜토리얼로, 일기를 쓰듯 시작하려는 기획을 짜놨다.
이에 자연스레 책 페이지가 넘어가는 효과를 구현하려 인터넷을 찾는데... 찾기가 쉽지 않았다.
유니티 무료 에셋 중에도 이런 효과를 구현한 에셋들이 있었지만, 오픈소스 라이센스가 걸려 있어 판매까지 노리는 우리 팀의 프로젝트에 선뜻 쓸 순 없었다.
물론 우리도 코드는 공개할 목적이지만. 그래도 이왕이면 저작권 걱정 없는 효과를 구현해서 나도 쓰고, 남들도 편하게 쓰게 하려는 게 이번 포스팅과 개발의 목적이다.
여기서 말하는 책 넘기기 효과란?
이런 효과를 구현하고 싶었다. 초반부에 바로 결과물이 나타나니 파악이 쉬울 것 같아 이 영상으로 가져왔다.
어떻게 만들어야 할까?
영어와 한글을 오가며 다양한 원리들을 보았다. 하지만 딱 이거다! 싶은 것은 크게 없었다. (3D를 이용하기도 했고, 유니티에 최적화되지 않은 것도 있었다.)
Unity3D Simple Page Curl Effect
Unity3D, 2D, Page Curl Effect, Page Flip Effect, UI, Canvas, 페이지 넘김 효과, 페이지 넘기기 page-curl effect with 2d mask tweak.유니티 UI의 Mask기능을 이용한 간단한 페이지 넘기기 예제입니다. 소스코드입니다. 의
gnupart.tistory.com
가장 비슷했던 건 이 블로그였지만, 파일 다운로드가 안 되어 구조를 제대로 파악할 수 없었다. 코드와 하이어라키 창도 있는데 만들기 꽤나 어려웠고, 이에 직접 만들려 했다.

마침 동아리방에 화이트보드가 있어, 직접 그리며 계산해보았다. 두 Quad를 겹치는 아이디어는 위의 블로그에서 얻었다.
기울어진 페이지를 Back이라고 하자.
위처럼 이리저리 삼각형의 닮음을 이용해 계산해봤다.
우리가 쉽게 얻을 수 있는 정보는 (x, y)다. 이는 모서리를 잡고 움직였을 때, 모서리의 위치다.
2θ 만큼 z축을 기울이면, 위와 같은 모양이 나옴을 확인했다. 이는 우측의 식대로 Atan(y / x)로 구할 수 있었다.
여기까지 코드를 짜고 테스트해보았다.
public Transform back;
public Vector2 point;
public Vector3 corner = new Vector3(600f, -450f, 0f);
public void Awake()
{
back = transform.GetChild(0);
corner += transform.localPosition;
Debug.Log(corner);
Debug.Log(back.transform.localPosition);
}
public void LateUpdate()
{
point = back.transform.localPosition;
// x, y 계산
float x = corner.x - point.x;
float y = point.y - corner.y;
// 세타 계산
// x == 0인 경우를 처리하기 위해, Atan이 아닌 Atan2를 쓴다.
float theta = -1 * Mathf.Atan2(y, x) * Mathf.Rad2Deg; ;
// 세타 적용
back.rotation = Quaternion.Euler(0f, 0f, 2 * theta);
}
UI와 Image를 이용했기에 transform이 깔끔하게 나오지 않았다. Debug와 함께 이리저리 바꿔보며, 제대로 계산되는 위치를 찾았다.
corner가 (600, -450, 0)인 이유는 전체 책의 크기가 (1200, 900)이며, 위치가 (0, 0)이기 때문이다. 즉, 우측 하단 코너의 위치다. 이를 책을 옮겨도 유지시키기 위해 Awake에서 책의 위치를 더해줬다.
책을 움직여야 한다면 Corner 오브젝트를 PageCurl의 하위에 넣고, 위치를 조정해줄 수도 있다. 혹은 width와 height를 이용해 할 수도 있을 것이다. 이건 찬찬히 고쳐보자.

보기엔 이상하지만 일단 한 걸음 나아갔다.
이렇게 돌아간 페이지엔 뒷면의 내용이 나와야 할 것이다. 그래서 이름을 Back으로 지었다.
반으로 자르기
위 움짤의 노란 부분은 두 가지가 합쳐진 부분이다.
- 하얀 페이지의 뒷면
- 책장을 넘긴 후의 페이지
그래서 이걸 분리해줘야 한다.
그렇다면, 책 페이지에서 어디를 기준으로 잘라내야 할까?
우선 아래의 그림을 보자.

아까와 같은 방법으로 새 페이지를 만들어 막아보자.
위처럼 계산하면, θ만큼 기울이면 되는 건 쉽게 알 수 있다.
이 경우의 문제는 얼마나 이동하냐(α)인데, 우리가 알아낸 정보를 이용하면 쉽게 계산할 수 있다.
(0, 0)부터 (x, y)의 거리를 2d라고 두자. 이때, α cos(θ) = d임을 위 그림으로부터 알아낼 수 있다.
그럼 α = d / cos(θ)이니, α만 구하면 저 사각형의 위치, 각도를 모두 구한 게 된다.
이제 다시 코드로 돌아가보자.
public Transform backMask;
public void CurlPage()
{
point = backPage.transform.localPosition;
// x, y 계산
float x = corner.x - point.x;
float y = point.y - corner.y;
// 세타 계산
// x == 0인 경우를 처리하기 위해, Atan이 아닌 Atan2를 쓴다.
float theta = Mathf.Atan2(y, x) * Mathf.Rad2Deg;
// BackPage 변경
backPage.rotation = Quaternion.Euler(0f, 0f, -2 * theta);
// BackMask 변경
backMask.rotation = Quaternion.Euler(0f, 0f, -theta);
// backMask의 이동할 거리 계산
float backMaskX = (Vector2.Distance(point, corner) / 2) / Mathf.Cos(theta * Mathf.Deg2Rad);
backMask.localPosition = corner - new Vector3(backMaskX, 0f, 0f);
}
뒷면을 가리는 마스크니 BackMask라고 이름짓고 코드를 짰다.

위아래, 양 옆에 마스크를 주어 불필요한 부분은 가려지게 했다.
이제야 책이 넘어가는 듯한 느낌이 난다.
마스크 적용하기
이제 파란 부분을 마스크로 처리해서, 저 부분엔 뒷면이 보이게 만들어야 한다.
그러려면 앞장과, 노란 뒷페이지는 파란 부분만 빼고 렌더링해야 한다.
처음엔 스텐실 버퍼 쪽으로 공부를 시작했지만, 하루~이틀 안에 완성시켜야 하는 상황에 처음 보는 개념, 게다가 URP의 버전 변화로 달라진 에셋 이름과 구성 덕에 차질이 많았다.
그래서 다음은 그나마 많이 써본 마스크를 사용하기로 했다.
유니티 - UI 이미지에 구멍뚫기
Mask
rito15.github.io
위 블로그에 단순하고 강력한 방법이 나와 있어, 이를 응용해 진행했다.
그래서 하이어라키 창의 구조가 아래와 같이 변경되었다.

각각의 역할은 아래와 같다.
Book: 책, 모든 페이지의 집합
Page: 하나의 페이지. 앞면(Front Page)과 뒷면(Back Page)으로 구성된다.
Mask: 마스킹 오브젝트. 위 링크와 관련 있으며, 뒷장의 내용이 보이게 한다.
각 오브젝트의 컴포넌트도 정리해보자.





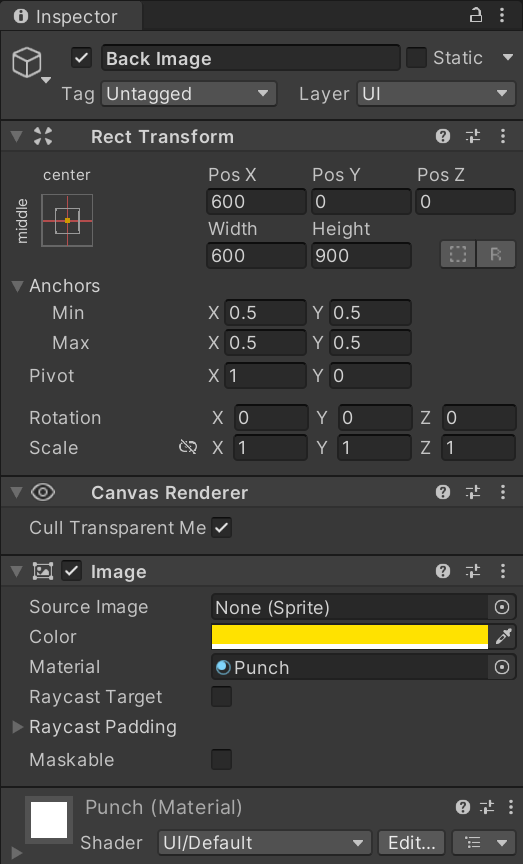
Page는 빈 오브젝트여서 생략했다. (추가하면 사진 길이가 너무 길어진다.)
MoveCorner 함수는 DOTween을 이용해 위치를 자연스럽게 움직인 코드다.
여기서 주의할 점은 크게 2가지
- Mask의 Color는 투명도(Alpha)가 1이다. 즉, (255, 255, 255, 1)이다. 투명도가 0이면 마스킹이 풀려버려서 1만 줬다.
- 두 Page의 Maskable 옵션이 꺼졌기 때문에, 마스크가 아닌 배경으로 가려야 한다.

그래서 Blocker를 사방에 두어 책 주위를 가렸다.
위치 고정시키기
위 방법의 치명적인 단점은, 이동하는 마스크가 최상위 부모이기에, 두 Page 오브젝트의 위치가 함께 변한다는 점이다.
이에 자식 오브젝트 위치 고정 등의 키워드로 검색을 진행했지만, 별다른 성과는 없었다.
자정이 넘어 집에 걸어오는 길에 문득 한 가지 방법이 떠올랐는데, 바로 위치를 저장해뒀다 복구하는 방식이다.
어렵지 않으니 바로 코드로 보자.
public void CurlPage()
{
point = backPage.transform.position;
// x, y 계산
float x = corner.x - point.x;
float y = point.y - corner.y;
// 세타(각도) 계산, 단위는 Degree(도)
// x == 0인 경우를 처리하기 위해, Atan이 아닌 Atan2를 쓴다.
float theta = Mathf.Atan2(y, x) * Mathf.Rad2Deg;
// BackPage, FrontPage가 Mask에 영향받아 움직이지 않게, 미리 위치를 캐싱해둔다.
Vector3 firstFrontPagePosition = frontPage.position;
Vector3 firstBackPagePosition = backPage.position;
// Mask의 이동할 거리 계산 및 이동
float maskX = (Vector2.Distance(point, corner) / 2) / Mathf.Cos(theta * Mathf.Deg2Rad);
mask.position = corner - new Vector3(maskX, 0f, 0f);
// Mask 회전
mask.rotation = Quaternion.Euler(0f, 0f, -theta);
// BackPage, FrontPage 위치를 원래대로 바꾼다.
backPage.position = firstBackPagePosition;
// BackPage의 회전은 계산한 결과대로 변경
backPage.rotation = Quaternion.Euler(0f, 0f, -2 * theta);
// FrontPage는 위치, 회전 고정
frontPage.position = firstFrontPagePosition;
frontPage.rotation = Quaternion.Euler(0f, 0f, 0f);
}
부모 오브젝트인 Mask가 움직일 때 자식 오브젝트들이 영향을 받는 것이니, 움직이기 직전 위치를 캐싱, 움직인 직후 복구하는 방법이다.
원래 rotation도 함께 저장해야 겠지만, backPage는 -2θ고 frontPage는 움직이지 않으니 저장하지 않았다.
기존처럼 로컬 좌표를 사용하면 의미가 없으니 전부 position으로 변경해줬고, 꽤나 고생했다.

그 덕에 꽤나 자연스러운 책 넘김 효과를 얻을 수 있었다. 꼭지점의 위치에 따라 실시간 계산되니, 사용도 Back Pivot만 옮기면 된다.
전체 코드
이제 전체 코드를 살펴보자.
using UnityEngine;
public class PageCurl : MonoBehaviour
{
public Transform backPage;
public Transform mask;
public Transform frontPage;
public Vector2 point;
public Vector3 corner = new Vector3(600f, -450f, 0f);
public void Awake()
{
backPage = transform.GetChild(0).GetChild(0).GetChild(0).GetChild(1);
frontPage = transform.GetChild(0).GetChild(0).GetChild(0).GetChild(0);
mask = transform.GetChild(0).GetChild(0);
corner += transform.position;
Debug.Log(corner);
Debug.Log(backPage.transform.position);
}
public void Update()
{
CurlPage();
}
public void CurlPage()
{
point = backPage.transform.position;
// x, y 계산
float x = corner.x - point.x;
float y = point.y - corner.y;
// 세타(각도) 계산, 단위는 Degree(도)
// x == 0인 경우를 처리하기 위해, Atan이 아닌 Atan2를 쓴다.
float theta = Mathf.Atan2(y, x) * Mathf.Rad2Deg;
// BackPage, FrontPage가 Mask에 영향받아 움직이지 않게, 미리 위치를 캐싱해둔다.
Vector3 firstFrontPagePosition = frontPage.position;
Vector3 firstBackPagePosition = backPage.position;
// Mask의 이동할 거리 계산 및 이동
float maskX = (Vector2.Distance(point, corner) / 2) / Mathf.Cos(theta * Mathf.Deg2Rad);
mask.position = corner - new Vector3(maskX, 0f, 0f);
// Mask 회전
mask.rotation = Quaternion.Euler(0f, 0f, -theta);
// BackPage, FrontPage 위치를 원래대로 바꾼다.
backPage.position = firstBackPagePosition;
// BackPage의 회전은 계산한 결과대로 변경
backPage.rotation = Quaternion.Euler(0f, 0f, -2 * theta);
// FrontPage는 위치, 회전 고정
frontPage.position = firstFrontPagePosition;
frontPage.rotation = Quaternion.Euler(0f, 0f, 0f);
}
}
CurlPage를 원하는 시점에 호출하기 위해 함수화 했었는데, 지금보니 귀퉁이를 움직이는 걸 실행해야 넘어간다.
그래도 Update 문에 그대로 적는 것보단 좋으니 유지했다.
마무리
나는 고정된 페이지 넘김 효과만 필요했기에(대화가 끝나면 자동으로 넘어간다.) 여기서 더 깔끔하게 선하진 않겠지만, 실제 무료 에셋들과 비교하면 부족한 점은 참 많다. 스텐실 버퍼를 쓰면 더 자연스러웠을 텐데. 라이센스만 아녔어도...
앞을 가려줘야 하고, 정해진 범위에서만 사용해야 하며, 1만큼 투명도를 남기는 등의 한계가 있지만, 이런 방법도 있구나 정도로 받아줬으면 좋겠다. 이 블로그에 올라온 코드들은 별도의 표기가 없다면 저작권을 행사하지 않을 것이니, 여러분의 개발에 한 톨이나마 도움이 되었다면 좋겠다.
다음 포스팅엔 그림자를 줘 좀 더 자연스럽게 만들고, 이를 여러 페이지로 늘리는 일을 해보겠다.
참고 자료
- 신바람 김박사TV, "AET#21 에펙 책넘기는 효과(CC Page Turn)", YouTube, 2021. 7. 9., https://www.youtube.com/watch?v=VypbILrN82Q
- GNUPart, "Unity3D Simple Page Curl Effect", 티스토리, 2015. 11. 16., https://gnupart.tistory.com/entry/Unity3D-Simple-Page-Curl-Effect
- Rito15, "유니티 - UI 이미지에 구멍뚫기", GitHub Pages, 2021. 9. 15., https://rito15.github.io/posts/unity-punch-ui-image/
'Unity > 로직 설계' 카테고리의 다른 글
| [Unity] CSV에서 자동으로 에셋 생성하기 (4) | 2024.08.28 |
|---|---|
| [Unity] 책 넘기는 효과 구현하기 (Page Curl) - 3 (0) | 2024.06.01 |
| [Unity] 책 넘기는 효과 구현하기 (Page Curl) - 2 (0) | 2024.06.01 |
| [Unity] InputAction 내 이벤트 초기화 (0) | 2023.02.24 |
| [Unity] DOTween - 회전하지 않고 물체 주위 맴돌기 (0) | 2022.11.06 |



